Vector projection
In order to understand more advanced concepts from vector operations it is good to have an intuition on such terms as vector projection.
Below is a two-dimensional example but its understanding will help us build intuition behind vector projection in any number of dimensions. So suppose we want to know the projection of vector $\overrightarrow{a}$ on vector $\overrightarrow{b}$:
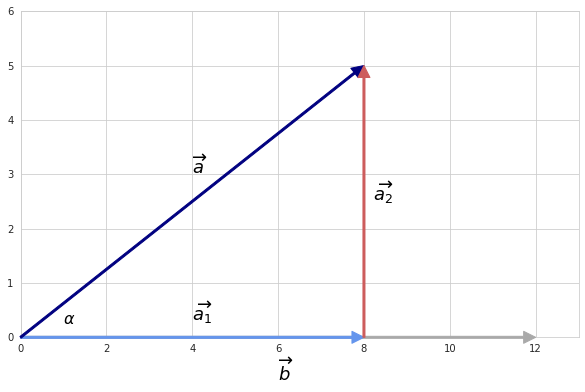
In this example we want to calculate vector $\overrightarrow{a_{1}}$ which has the same direction as vector $\overrightarrow{b}$ but the length of which is restricted by the span of vector $\overrightarrow{a}$ in the direction of $\overrightarrow{b}$.
Let’s recall that in rectangular triangle cosine of an angle is the ratio between the adjacent side and the hypotenuse. Therefore, $||a_{1}||$, known as scalar projection, can be expressed as $||a|| \cos{\alpha}$, where $\alpha$ is the angle between $\overrightarrow{a}$ and $\overrightarrow{b}$. The vector projection will be equal to the scalar projection multiplied by direction of $\overrightarrow{b}$:
$\overrightarrow{a_{1}} = \lVert a_{1}\rVert\frac{b}{\lVert b\rVert} = \lVert a\rVert \cos{\alpha}\frac{b}{\lVert b\rVert}$
The direction of $\overrightarrow{b}$ is a unit vector expressed as a scaled version of $\overrightarrow{b}$.
Cosine calculation
When $\alpha$ is not known the cosine of $\alpha$ can be be expressed as follows:
$\cos{\alpha} = \frac{\overrightarrow{a} \cdot \overrightarrow{b}}{\lVert a\rVert \cdot \lVert b\rVert}$,
where $\overrightarrow{a} \cdot \overrightarrow{b}$ is the dot product of two vectors.
The formula is based on the Law of cosines which states that for any triangle the following holds true:
$c^{2} = a^{2} + b^{2} - 2ab \cos{\alpha}$
In terms of vectors of our example we can write it down like this:
$\lVert a_2\rVert^2 = \lVert a\rVert^2 + \lVert a_1\rVert^2 - 2 \lVert a\rVert \lVert a_1\rVert \cos{\alpha}$,
where $\overrightarrow{a_2}$ can be expressed as $\overrightarrow{a} - \overrightarrow{a_1}$.
$(\lVert a - a_1\rVert) (\lVert a - a_1\rVert) = \lVert a\rVert^2 + \lVert a_1\rVert^2 - 2 \lVert a\rVert \lVert a_1\rVert \cos{\alpha}$
$\lVert a\rVert^2 + \lVert a_1\rVert^2 - 2 \overrightarrow{a} \cdot \overrightarrow{a_1} = \lVert a\rVert^2 + \lVert a_1\rVert^2 - 2 \lVert a\rVert \lVert a_1\rVert \cos{\alpha}$
$\overrightarrow{a} \cdot \overrightarrow{a_1} = \lVert a\rVert \lVert a_1\rVert \cos{\alpha}$
The key takeaway from it is that the dot product of two vectors is useful in calculation of vector projection. Other than that it is measure of similarity of two vectors.